Rekursionen sind etwas schwierig zu verstehen aber ungeheuer mächtig. In allen Situationen, in denen auf baumähnlichen Strukturen gearbeitet werden, ist eine Rekursion kaum zu umgehen.
- Countdown
- Fibonacci
- Fakultät
- Sinn und Unsinn rekursiver Funktionen
- Beispiel: Einbindung von Dateiinhalten
- Beispiel: binärer Baum
- Türme von Hanoi
- Videos
- Beispiel: Taschenrechner
Countdown
Das folgende Beispiel erzeugt, wie der Name der Methode schon vermuten lässt, einen Countdown. Die Methode gibt den übergebenen Wert auf dem Bildschirm aus und ruft sich selbst mit dem um 1 verminderten Parameter auf.
// Java
class CountDown {
static void countDown(int n) {
if (n>0) {
System.out.println(n);
countDown(n-1);
}
}
public static void main(String[] args) {
countDown(10);
}
}
// C/C++
#include <iostream>
void countDown(int n)
{
if (n>0)
{
std::cout << n << std::endl;
countDown(n-1);
}
}
int main()
{
countDown(10);
}
Die Wiederholung erfolgt nicht durch eine Schleife, sondern dadurch, dass sich die Methode countDown selbst aufruft - die sogenannte Rekursion.
Jeder Aufruf einer Methode führt dazu, dass die Aufrufposition gespeichert wird, damit die Methode dorthin zurückkehren kann. Neben der Rücksprungadresse werden dort auch alle lokalen Variablen inklusive der Parameter wieder hergestellt, so dass der Rücksprung in die ursprüngliche Situation möglich ist.
Wie jede Schleife muss auch die Rekursion ein Ende haben. Dazu muss die Endebedingung sauber formuliert werden. Ansonsten kommt es zu einer Endlosschleife. Im Falle einer Rekursion läuft dann der Stapelspeicher über, der die Rücksprungadresse und die lokalen Variablen aufnimmt, der sogenannte Stack-Overflow.
Im Falle des Countdowns wird die Endebedingung durch die if-Anweisung definiert, die vor dem rekursiven Aufruf steht.
Beim Selbstaufruf von countDown wird irgendwann der Parameter 0 und die Abfrage greift nicht mehr. Stattdessen kehrt die Methode zu ihrem Aufrufer zurück, der eben sie selbst ist. Aber dort passiert nichts mehr. Sie läuft auch hier auf das Methodenende. Das geschieht so lange, bis sie zu ihrem Aufrufer zurückkehrt.
Nutzung des Stacks
Eine Rekursion nutzt den Stack, in dem bei jedem Funktionsaufruf die Rücksprungadresse, die lokalen Variablen und die Parameter abgelegt werden. Wenn die Funktion ohne Seiteneffekte programmiert wurde, enthält der Stack den kompletten Zustand des bisherigen Funktionsablauf. Ruft sie sich selbst mit anderen Parametern auf, wird der bisherige Zustand auf dem Stack erhalten, quasi eingefroren. Oben auf dem Stack wird für die neue Funktion wieder eine neue Umgebung geschaffen. Endet die Funktion, wird deren Umgebung vom Stack gelöscht und sie kehrt zu dem eingefrorenen Zustand wieder zurück.Umgekehrt
Tauscht man die beiden Zeilen hinter der Abfrage aus, zählt die Mehode von 1 bis 10. Das liegt daran, dass nun die Methode die Ausgabe erst erreicht, wenn sie bis zum Ende abgestiegen ist. Erst wenn der Parameter 0 ist, kehrt die Methode zurück, springt hinter den Aufruf und erreicht dort System.out.println. Damit wird dann 1 ausgegeben. Der Rücksprung kommt in die Methode, wo n noch 2 war und so geht es weiter.
// Java
class CountDown {
static void countDown(int n) {
if (n>0) {
countDown(n-1);
System.out.println(n);
}
}
public static void main(String[] args) {
countDown(10);
}
}
// C/C++
#include <iostream>
void countDown(int n)
{
if (n>0)
{
countDown(n-1);
std::cout << n << std::endl;
}
}
int main()
{
countDown(10);
}
Fakultät
Im Internet oder in der Literatur finden Sie als Beispiel für rekursive Programme oft die Fakultät. Die Fakultät von n berechnet sich durch das Produkt einer Reihe.fakultaet(n) = 1 * 2 * ... * n
Die Berechnung kann rekursiv erfolgen. Dabei errechnet man die Fakultät von n als die Multiplikation von n mit der Fakultät von (n-1) und so weiter. Damit ergibt sich eine Funktion folgender Art:
long fakultaet(int n) {
if (n>1) {
return n * fakultaet(n-1);
}
return 1;
}
Das funktioniert natürlich. Man muss aber zugeben, dass die Berechnung der
Fakultät auch iterativ - also per Schleife - funktioniniert, schneller ist
und für die meisten Programmierer leichter zu verstehen ist.
Und sehr viel länger wird die Funktion auch nicht:
long iterfakultaet(int n) {
long f = 1;
for (int i=2; i<=n; i++) {
f = f * i;
}
return f;
}
Fibonacci
Was sind die Fibonacci-Zahlen?Die Fibonacci-Folge ist eine Folge ganzer Zahlen, in der sich jedes Element aus der Summe seiner beiden Vorgänger bildet.
fibonacci(n) = fibonaci(n-1) + fibonaci(n-2)
Für Youtube-Fans hier die Erklärung von Christian Spannagel.
Die Bildung eines Elements der Folge über deren Vorgänger nennt man rekursiv. In C/C++ oder Java ausgedrückt ergibt sich folgende Funktion:
int fibonacci(int n)
{
if (n <= 1)
return 1;
else
return fibonacci(n-1) + fibonacci(n-2);
}
Diese Art der Berechnung ist sehr analog zur mathematischen Definition.
Aber auch die Fibonacci-Folge ist recht einfach iterativ zu berechnen.
long iterfibonacci(int n) {
long a = 1, b = 1, f = 1;
for (int i=1; i<n; i++) {
f = a + b; a = b; b = f;
}
return f;
}
Bei einem Vergleich der beiden Verfahren stellt sich heraus, dass die
rekursive Lösung bei höheren Zahlen extrem langsam wird (etwa 50).
Das ist bei der iterativen Variante nicht feststellbar.
Der Grund dafür ist, dass jeder Aufruf der Funktion zwei rekursive Aufrufe
durchführt, die jeweils wiederum zwei Aufrufe durchführen. Das schaukelt sich
extrem schnell hoch.
Sinn und Unsinn rekursiver Funktionen
Die bisherigen Beispiele ließen sich auch durch Schleifen realisieren und sind dann sogar oft wesentlich schneller. Was soll es also, sich mit der Rekursion zu befassen? Tatsächlich ist der Einsatz für lineare Probleme wenig sinnvoll.Sobald es aber um Probleme geht, die auf baumartigen Strukturen basieren, geht an der Rekursion kein vernünftiger Weg vorbei.
+----+
| 12 |
+----+
/ \
+----+ +----+
| 7 | | 17 |
+----+ +----+
/ \ \
+----+ +----+ +----+
| 3 | | 9 | | 22 |
+----+ +----+ +----+
/
+----+
| 2 |
+----+
Es zeigt sich wieder einmal, dass es um das biologische Wissen der meisten
Informatiker betrüblich aussieht: Die Wurzel des Baums ist oben.
Im vorliegenden Fall liegt in der Wurzel die 12. Nach links enthalten alle
Knoten kleinere, nach rechts größere Werte.
Das gilt in diesem Baum für alle
Knoten. Sind die Informationen wie hier sortiert angeordnet, dann können
sie extrem schnell gefunden werden.
Wie würden Sie beispielsweise einen binären Baum wie den obigen mit einer normalen Schleife durchlaufen? Eine rekursive Funktion dafür ist recht kurz.
void ausgeben(Knoten knoten) {
if (knoten.links!=null) {
ausgeben(knoten);
}
System.out.println(knoten.zahl);
if (knoten.rechts!=null) {
ausgeben(knoten);
}
}
- Solange auf dem linken Ast noch ein Knoten folgt, wird die Funktion sich selbst mit diesem Nachfolger aufrufen. Zuvor wird sie ihre Position im Programm und die lokalen Variablen inklusive Parameter auf dem Stack speichern. Kommt sie also vom Aufruf zurück, ist alles wie zuvor.
- Hat sich die Funktion oft genug aufgerufen, landet sie bei der 2. Hier gibt es keinen linken Nachfolger. Es gibt keinen rekursiven Aufruf mehr.
- Nun wird die Ausgabe (System.out.prinln) der Zahl des Knotens auf dem Bildschirm ausgegeben.
- Anschließend wird geprüft, ob es einen rechten Ast gibt.
- Das ist nicht der Fall. Die Funktion endet und springt in den Zustand hinter dem Aufruf, als sie auf dem Knoten mit der 3 stand. Die 3 wird ausgegeben. Einen rechten Ast gibt es nicht. Die Funktion kehrt zurück.
- Nun ist sie wieder im Zustand, als sie den Knoten mit der 7 bearbeitete. Sie gibt die 7 aus.
- Hier gibt es einen rechten Ast. Sie ruft sich mit dem Knoten mit der 9 auf.
- Diese hat keinen linken Ast, sonst würde sie ihn hinabsteigen.
- Stattdessen gibt die Funktion die 9 aus, stellt keinen rechten Ast fest und kehrt zurück.
- Der Rest des Baums wird auf diese Weise abgearbeitet. Tatsächlich wird der gesamte Baum sauber durchlaufen.
Beispiel: Einbindung von Dateiinhalten
In der Programmiersprache C (und auch in C++) gibt es den Präprozessorbefehl #include. Er fordert den Präprozessor auf, die danach aufgeführte Datei zu laden und auszuwerten. Das wird vor allem für Deklarationen verwendet. Solche include-Dateien enthalten oft weitere include-Befehle. Es ergibt sich ein Baum von Dateien, die der Präprozessor auswerten muss.Mit Schleifen bekommen Sie das nur schwer in den Griff, da das Programm nach Auswertung einer Datei an die Stelle zurückkehren muss, an der es zuletzt gewesen ist. Das folgende Skelett einer Funktion zeigt, wie das Problem durch eine Rekursion zu lösen ist.
include(char * DateiName)
{
oeffneDatei(DateiName)
while (!endeDerDatei())
{
liesZeile();
if (enthaeltInclude(IncludeDateiName))
{
include(IncludeDateiName);
}
werteAus();
}
schliesseDatei();
}
Eine solche Funktion kommt mit beliebig verschachtelten #include-Befehlen zurecht. Übrigens finden Sie bei TeX bzw. LaTeX mit dem Befehl input einen ähnlichen Befehl.
Beispiel: binärer Baum
Binäre Bäume lassen sich am einfachsten per Rekursion bearbeiten. Ein binärer Baum besteht aus Knoten, die jeweils zwei Äste besitzen, die wiederum auf einen weiteren Knoten zeigen. Jeder Knoten enthält eine Information.Um einen Baum in einem Programm nachzubilden, muss ein Knoten beschrieben werden und die Knoten untereinander in Baumform verbunden werden. Die Datenstruktur eines Knotens hat folgendes Aussehen:
Knoten eines Binärbaums
struct Knoten
{
int zahl;
Knoten * links;
Knoten * rechts;
};
public class Knoten {
public int zahl;
public Knoten links;
public Knoten rechts;
}
Ein Baum entsteht, wenn mehrere Knoten durch die Zeiger links oder rechts miteinander verbunden werden. Ein Knoten wird mit dem Befehl new erzeugt. Der Rückgabewert ist der Zeiger auf den neuen Knoten. Um auf die Elemente des Knotens zuzugreifen, wird in C/C++ an den Zeigernamen die Zeichenkombination -> gefolgt vom Elementnamen angehängt, in Java werden beide durch einen Punkt getrennt. Das Hauptprogramm soll einen Baum aufbauen, indem die Funktion einfuegen für alle Elemente eines Arrays aufgerufen wird. Zum Test soll der Baum dann ausgegeben werden.
int main()
{
Knoten *baum = new Knoten;
baum->zahl = 12;
int zahlen[6] = { 7, 17, 3, 9, 22, 2 };
for (int i=0; i<6; i++)
{
baum = einfuegen(baum, zahlen[i]);
}
ausgeben(baum);
}
public static void main(String[] args) {
int zahlen[] = { 7, 17, 3, 9, 22, 2 };
Knoten baum = new Knoten();
baum.zahl = 12;
for (int zahl : zahlen) {
baum = einfuegen(baum, zahl);
}
ausgeben(baum);
}
Binärbaum füllen
Auch das Einfügen in den Baum ist am einfachsten rekursiv zu lösen. Dabei wird zunächst das Blatt gesucht, dessen Nachfolger der neue Eintrag werden soll. Diese Stelle muss ein Null-Zeiger sein.An dieser Stelle wird ein neues Blatt eingehängt. Das ist auch gleichzeitig das Rekursionsende. Hier wird das neue Element in den Baum eingefügt und die Adresse des Blatts zurückgegeben, damit es vom Aufrufer in den Baum eingehängt wird.
Knoten * einfuegen(Knoten *blatt, int zahl)
{
if (blatt==0) // Freie Position gefunden
{ // Neues Blatt einfügen
blatt = new Knoten;
blatt->links = blatt->rechts = 0;
blatt->zahl = zahl;
return blatt; // Zeiger auf neues Blatt zurückgeben
}
if (zahl < blatt->zahl)
{ // Zuweisung behält altes Blatt oder das neue
blatt->links = einfuegen(blatt->links, zahl);
}
else if (zahl > blatt->zahl)
{ // Zuweisung behält altes Blatt oder das neue
blatt->rechts = einfuegen(blatt->rechts, zahl);
}
return blatt; // gib das aktuelle Blatt zurück
}
static Knoten einfuegen(Knoten blatt, int inhalt)
{
if (blatt==null) // Freie Position gefunden
{ // Neues Blatt einfügen
blatt = new Knoten();
blatt.links = blatt.rechts = null;
blatt.zahl = inhalt;
return blatt; // Zeiger auf neues Blatt zurückgeben
}
if (inhalt < blatt.zahl)
{ // Zuweisung behält altes Blatt oder das neue
blatt.links = einfuegen(blatt.links, inhalt);
}
else if (inhalt > blatt.zahl)
{ // Zuweisung behält altes Blatt oder das neue
blatt.rechts = einfuegen(blatt.rechts, inhalt);
}
return blatt; // gib das aktuelle Blatt zurück
}
blatt->links = einfuegen(blatt->links, zahl);
In den meisten Fällen wird diese Zuweisung den Knoten nicht verändern, weil der als erster Parameter übergebene Knoten exakt der ist, der vorher an dieser Stelle im Baum stand. Nur wenn blatt->links 0 war, dann wird ein neuer Knoten erzeugt. Der Zeiger auf den neuen Knoten wird zurückgegeben und an dieser Stelle in den Baum eingehängt.
Auslesen
Das Auslesen eines binären Baums ist zuvor bereits gezeigt worden.
void ausgeben(Knoten *knoten) {
if (knoten->links) {
ausgeben(knoten->links);
}
std::cout << knoten->zahl << std::endl;
if (knoten->rechts) {
ausgeben(knoten->rechts);
}
}
static void ausgeben(Knoten knoten) {
if (knoten.links!=null) {
ausgeben(knoten.links); // -- pos1 --
}
System.out.println(knoten.zahl);
if (knoten.rechts!=null) {
ausgeben(knoten.rechts); // -- pos2 --
}
}
Übung
- Schreiben Sie eine rekursive Funktion, die Zahlen in einem Binärbaum sucht.
Türme von Hanoi
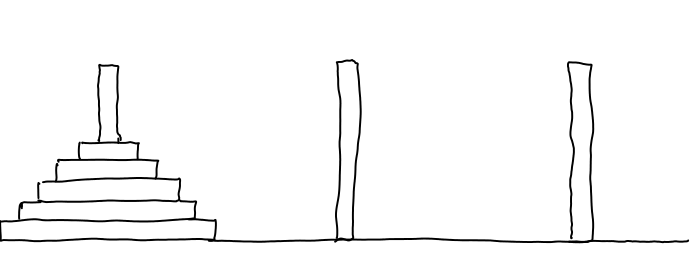
Ein etwas überraschendes Beispiel für eine Rekursion sind die Türme von Hanoi. Das Ziel dieses Geduldspiels mit den drei Stäben ist es, die wohlgeordneten Scheiben auf dem linken Stab auf den rechten Stab zu bringen. Das wird erst dadurch schwierig, dass immer nur eine Scheibe bewegt und niemals eine größere Scheibe auf einer kleineren liegen darf. Die folgenden Abbildung zeigt die Ausgangsposition.
Vollständige Induktion
Es gibt einen Beweis, dass das Spiel für beliebig viele Scheiben immer lösbar ist. Dazu wird die vollständige Induktion verwendet. Und diese ist gleichzeitig der Lösungsansatz, wie die Aufgabe rekursiv zu lösen ist. Der Beweis vollzieht sich in zwei Schritten.- Verankerung:
- In der Verankerung der vollständigen Induktion wird gezeigt, dass das Problem für 1 lösbar ist. Wenn der Turm nur aus einer Scheibe besteht, kann man diese einfach vom linken Stab auf den rechten legen. Das war also ganz leicht.
- Induktionsschritt:
-
Es muss gezeigt werden, dass wenn es für eine beliebige Zahl n gilt,
auch für n+1 gilt.
Es wird also bewiesen, dass man einen Turm aus n+1 Scheiben korrekt umsetzen kann, sofern dies für n Scheiben funktioniert. Wir gehen von der Situation aus, dass sich auf dem linken Stab n+1 Scheiben befinden.
Die obersten n Scheiben werden auf den mittleren Stab gesetzt. Nach der Voraussetzung ist das ja möglich.
Auf dem linken Stab verbleibt eine Scheibe, die auf den dritten Stab verlegt wird. Der ist ja noch leer.
Dann werden die n Scheiben vom mittleren Stab auf den rechten Stab gelegt. Anschließend liegen n+1 Scheiben auf dem rechten Stab.
Damit ist bewiesen, dass n+1 Scheiben umgesetzt werden können, wenn es möglich ist, n Scheiben regelkonform zu versetzen.
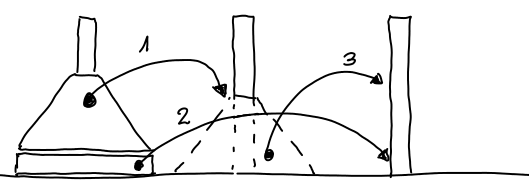
Damit ist es bewiesen, dass man die Türme von Hanoi lösen kann, egal wie viele Scheibe auf dem linken Stab sind. Für 1 haben wir es gezeigt. Wenn 1 geht, dann muss aus dem Induktionsschritt folgen, dass 1+1, also 2 auch geht. Dann geht es auch für 3 und so weiter.
Programm
Die rekursive Funktion Ziehe() realisiert genau den Induktionsschritt. Sie prüft zunächst das Rekursionsende. Das tritt ein, wenn keine Scheibe mehr vorliegt. Dann ruft sie sich selbst mit n-1 Scheiben auf, um den Stapel vom Ausgangsstab zum freien Stab zu verschieben. Danach wird die unterste Scheibe verschoben. Das wird einfach durch die Bildschirmausgabe realisiert. Es wird angezeigt, von welchem Stab zu welchem Stab die Scheibe umgesetzt werden muss. Danach werden die n-1 Scheiben auf die große Scheibe gesetzt. Dazu ruft die Funktion wieder sich selbst auf.Freiplatz
Der freie Platz wird mit einem kleinen Trick bestimmt. Die Funktion weiß durch die Parameter, welche Stäbe belegt sind. Der übrige Stab muss frei sein. Auf diesen muss der Reststapel versetzt werden. Die Summe der Stabnummern ist immer 1+2+3=6. Wenn zwei der Stäbe bekannt sind, brauchen Sie sie nur addieren, und der dritte muss die Differenz zu 6 sein.
#include <iostream>
using namespace std;
void Ziehe(int von, int nach, int ScheibenZahl)
{
int frei;
if (ScheibenZahl==0) return;
frei = 6 - von - nach; // bestimme den freien Platz
Ziehe(von, frei, ScheibenZahl-1);
cout << von << " - " << nach << endl;
Ziehe(frei, nach, ScheibenZahl-1);
}
int main()
{
Ziehe(1, 3, 3); // von 1 nach 3, 3 Scheiben
}
public class Hanoi {
static void hanoi(int scheiben, char start, char end, char mitte) {
if (scheiben == 1){
System.out.println("von "+start+" nach "+end);
} else {
hanoi(scheiben - 1, start, mitte, end);
System.out.println("von "+start+" nach "+end);
hanoi(scheiben - 1, mitte, end, start);
}
}
static public void main(String[] args){
hanoi(3, 'A', 'B', 'C');
}
}
Der erste Aufruf zeigt, dass die Scheiben zunächst auf Stab 1 liegen, dass sie auf Stab 3 versetzt werden sollen und dass es drei Scheiben sind. Das Programm zeigt das folgende Ergebnis:
1 - 3 1 - 2 3 - 2 1 - 3 2 - 1 2 - 3 1 - 3Um also das Spiel für drei Scheiben zu lösen, legen Sie zunächst die Scheibe von Stab~1 auf Stab~3. Dann wird die nächste Scheibe von Stab~1 auf Stab~2 gelegt. Wenn Sie dieser Anleitung folgen, können Sie das Spiel auflösen.
Beispiel: Taschenrechner
Auch im Compilerbau werden Rekursionen intensiv eingesetzt. Als Beispiel wird hier ein Programm vorgestellt, das einfache Rechenaufgaben lösen kann. Das Programm wertet eine Zeichenkette aus.Wenn Sie diese Funktionen in Ihr Programm für die Zahleneingabe einbauen, können Anwender auch einfache Grundrechenarten eingeben, wie sie sie aus Tabellenkalkulationen kennen.
Die erste Stufe ist die so genannte lexikalische Analyse. Hier werden Textelemente wie Rechenoperatoren oder Zahlenkonstanten identifiziert und zu Tokens zusammengefasst.
Token
Der Aufzählungstyp tToken enthält die Symbole. Neben den vier Grundrechenarten (PLUS, MINUS, MUL, DIV) sind dies die Klammern (LPAR und RPAR) und die Zahlen (NUMBER). Das Symbol END zeigt das Eingabeende an, und das Symbol ERROR wird benötigt, um Eingabefehler zu kennzeichnen.sucheToken()
Die Funktion sucheToken() erkennt die Symbole und ist in der Lage, einen ganzzahligen Wert zu ermitteln. Hier wird noch keine Rekursion benötigt.
enum tToken
{
PLUS, MINUS, MUL, DIV, LPAR, RPAR, NUMBER, END, ERROR
};
// Globale Variablen:
tToken aktToken; // das zuletzt erkannte Token
double TokenZahlenWert; // der Wert bei Zahlenkonstanten
char *srcPos; // Programm-Position
tToken sucheToken()
// Sucht ab der aktuellen Stringposition das nächste Token.
// Hier werden auch die Zahlenkonstanten bestimmt und in
// der globalen Variablen TokenZahlenWert abgelegt.
{
aktToken = ERROR;
if (*srcPos==0)
{
aktToken = END;
}
else
{
switch (*srcPos)
{
case '(': aktToken=LPAR; break;
case ')': aktToken=RPAR; break;
case '*': aktToken=MUL; break;
case '/': aktToken=DIV; break;
case '+': aktToken=PLUS; break;
case '-': aktToken=MINUS; break;
}
if (*srcPos>='0' && *srcPos<'9')
{
aktToken=NUMBER;
TokenZahlenWert = 0.0;
}
while (*srcPos>='0' && *srcPos<'9')
{
TokenZahlenWert *= 10;
TokenZahlenWert += *srcPos-'0';
srcPos++;
}
if (aktToken != NUMBER)
{
srcPos++;
}
}
return aktToken;
}
tToken Error(char *s)
// Meldung ausgeben und Fehler-Token zurückliefern
{
cerr << s << endl;
return ERROR;
}
Die Rekursion wird erst verwendet, wenn das Programm beginnt, die Tokens als Anweisungen zu interpretieren und dabei Klammern und Prioritäten berücksichtigt.
Zuerst wird die Funktion aufgerufen, die die Operation mit der niedrigsten Priorität auswertet. Das ist im Beispiel die Funktion PlusMinus(). Diese ruft sofort die Behandlung der Punktrechnung in der Funktion MulDiv() auf. Und auch diese Funktion wendet sich zuerst an die Funktion Klammern(). Die Klammern haben wie die Vorzeichen die höchste Priorität.
Entsprechend prüft die Funktion Klammern(), ob ein Token vorliegt, das ihrer Prioritätsstufe entspricht. Dazu gehört die öffnende Klammer, eine Zahl oder ein Vorzeichen. Ist das vorliegende Token keines dieser Elemente, endet die Funktion und springt somit zur aufrufenden Funktion MulDiv() zurück. Diese schaut nach dem Stern oder dem Schrägstrich. Erst wenn auch das nicht passt, kehrt der Aufruf wieder zu PlusMinus() zurück und wertet die Addition oder Subtraktion aus.
Rekursiver Abstieg
Wenn aber die Funktion Klammern() fündig geworden ist und eine linke Klammer gefunden hat, dann ruft sie PlusMinus() auf, um den eingeklammerten Ausdruck zu analysieren. Da die Funktion Klammern() durch PlusMinus() aufgerufen wurde, handelt es sich hier um eine indirekte Rekursion.
double PlusMinus(); // Prototyp
double Klammern()
// wertet Klammern, Zahlen und Vorzeichen aus
// ruft Klammern() und PlusMinus() dadurch rekursiv auf!
{
double Wert;
switch(aktToken)
{
case NUMBER:
sucheToken();
return TokenZahlenWert;
case MINUS:
sucheToken();
return -Klammern();
case LPAR:
sucheToken();
Wert = PlusMinus();
if (aktToken != RPAR)
{
return Error(") expected");
}
sucheToken();
return Wert;
case END:
return 1;
}
return Error("primary expected");
}
double MulDiv()
// wertet Multiplikation und Division aus
// ruft Klammern() auf, dadurch rekursiv!
{
double Wert;
// rufe erst die Operation mit der nächsthöheren
// Priorität auf
Wert = Klammern();
while (aktToken==MUL || aktToken==DIV)
{
if (aktToken==MUL)
{
sucheToken();
Wert *= Klammern();
}
else if (aktToken==DIV)
{
sucheToken();
Wert /= Klammern();
}
}
return Wert;
}
double PlusMinus()
// wertet Summe und Differenz aus
// ruft MulDiv() auf, dadurch rekursiv
{
double Wert;
// rufe erst die Operation mit der nächsthöheren
// Priorität auf
Wert = MulDiv();
while (aktToken==PLUS || aktToken==MINUS)
{
if (aktToken==PLUS)
{
sucheToken();
Wert += MulDiv();
}
else if (aktToken==MINUS)
{
sucheToken();
Wert -= MulDiv();
}
}
return Wert;
}
double Auswertung(char *s)
{
srcPos = s;
sucheToken(); // bestimme das erste Token vorweg
return PlusMinus();
}
int main(int argc, char* argv[])
{
double Wert = Auswertung(argv[1]);
cout << Wert << endl;
return 0;
}
Der Aufruf der Funktion Auswertung() erfordert als Parameter nur die Zeichenkette, in der sich der auszuwertende Ausdruck befindet. Die Eingabe darf keine Leerzeichen enthalten und ist auf ganzzahlige Eingaben beschränkt, da die Funktion sucheToken() derzeit keine Nachkommastellen auswertet.
Aufruf
Das Programm erhält seinen auszuwertenden String als ersten Parameter. Unter UNIX ist darauf zu achten, dass Sie diesen in Anführungszeichen setzen, sobald Sie eine Multiplikation ausführen wollen. Der Grund ist, dass die Shell einen Stern als Platzhalter für Dateien interpretieren wird und dadurch drollige Ergebnisse zu erwarten sind.Hier sehen Sie ein paar Testläufe:
> calc "12*(5+2)" 84 > calc "4*(5+2)" 28 > calc "4*5+2" 22 > calc "(5-4)*5*6+(7-3)*((4+2))" 54 > calc "(5-4)*5*6+(7-3)*((4+5)/3)" 42 >
Der Rechner kommt mit der Punkt-vor-Strich-Regel klar, hat kein Problem mit Klammern und kann auch komplexere Ausdrücke ausrechnen.
Videos
Rekursionen
Rekursionen T.2 Bäume
Übungsaufgaben
- An anderer Stelle finden Sie ein Beispiel, wie Sie aus einer Zeichenkette Fließkommazahlen auslesen. Integrieren Sie dies in den kleinen Taschenrechner, damit er auch mit Werten vom Typ double umgehen kann.
- Ergänzen Sie den Taschenrechner dahingehend, dass in der Eingabe auch Leerzeichen zwischen den Tokens stehen können. Beim Test sollten Sie die Eingaben mit Leerzeichen in Anführungszeichen setzen. Ansonsten wird Ihre Eingabezeile auf mehrere Parameter verteilt.
- Warum kommt der Interpreter mit dem Minus nicht durcheinander, obwohl es einmal als Vorzeichen und einmal als Operator verwendet wird?