Python in Naturwissenschaft und Mathematik
Willemers Informatik-Ecke

NumPy

Mit dem Modul NumPy lassen sich Vektoren und Matrizen direkt verarbeiten.

Installation

Im Internet findet man die Seite von NumPy unter der URL https://numpy.org. Dort können Sie das Paket auch kostenlos herunterladen.

Linux-Anwender können sich das Paket aber auch direkt aus dem System-Repository installieren. 

apt install python3-numpy

Array alias Vector

In dem folgenden Beispiel wird das Array zahlen durch die Liste der Zahlen von 1 bis 6 initialisiert. Dieses Array wird als Parameter für die Sinusfunktion sin übergeben. Diese Funktion sin stammt aus dem Paket numpy und erzeugt ein gleich großes Array (sinvec), das die Sinuswerte für alle Werte des übergebenen Arrays erzeugt. 
import numpy as np
zahlen = np.array([1, 2, 3, 4, 5, 6])
sinvec = sin(zahlen)
sinvec = np.sin(zahlen)
print(sinvec)
Als Ergebnis erscheint: 
[ 0.84147098  0.90929743  0.14112001 -0.7568025  -0.95892427 -0.2794155 ]
Anstatt die Zahlenwerte eines Arrays vorzugeben, kann das Array mit der Funktion arange aber auch erzeugt werden. Die Parameter sind: Das folgende Array sinwerte wird also eine komplette Sinuswelle enthalten. Sie startet bei 0 und endet bei 2π. Die Schrittweite von 0.1 ergibt damit die Abtastrate der Funktion. 
sinwerte = np.arange(0.0, 2*np.pi, 0.1)
Soll das Array nur mit Nullen gefüllt sein, hilft die Funktion zeros. Das Array nullvec wird mit 12 Elementen angelegt, die alle mit 0 vorbesetzt werden. 
nullvec = np.zeros(12)
Ein Array kann auch mit Zufallszahlen gefüllt werden. 
zufall = np.random.rand(7)
Mit der Funktion randn wird das Array mit gauß'schen Zufallszahlen gefüllt. 
zufall = np.random.randn(7)
Die mathematischen Operatoren können auch auf Arrays angewandt werden. Ein Pluszeichen bewirkt dann eine Vektorenaddition.

Lineare Gleichungssysteme

In mehrere Flaschen und Gläser kann ich insgesamt 2,9 Liter Flüssigkeit einfüllen. Jede Flasche kann 0,7 Liter und jedes Glas nimmt 0,2 Liter auf.

Für die Flaschen zahle ich 50 Cent Pfand, für jedes Glas 0,80 Cent. Insgesamt sind es 4,70.

Daraus ergibt sich folgendes Gleichungssystem:

x Flaschen * 0,7 + y Gläser * 0,2 ergeben 2,9 Liter Inhalt.
x Flaschen * 0,50 + y Gläser * 0,80 kosten 4,70

Daraus ergibt sich folgendes Programm 

import numpy
  
matrix = numpy.array([[0.7, .2],[0.5, .8]])
lsgvec = numpy.array([[2.9], [4.7]])
anzahl = numpy.linalg.solve(matrix, lsgvec)
print(anzahl)
Das Programm gibt aus: 
[[ 3.]
 [ 4.]]
Es sind drei Flaschen und vier Gläser.

Skalarprodukt

a und b seien Vektoren der Länge n. Dann ist das Skalarprodukt:

ab = a1b1 + a2b2 + ... + anbn

NumPy bietet zur Errechnung des Skalarprodukts zweier Vektoren die Funktion dot an. 

import numpy

skalarprodukt = numpy.dot(a, b)

Matrixmultiplikation

Hat die Matrix a gleich viele Spalten wie die Matrix b Zeilen hat, ergibt die die Multipliation eine Matrix c mit der Anzahl der Zeilen von a und der Anzahl der Spalten von b.

Die Felder ergeben sich aus folgender Rechnung:

cik = ∑ aij bjk 

import numpy
a = numpy.matrix( ((1,3), (4,2), (1,2), (3,1)) )
b = numpy.matrix( ((2,3,3), (1,2,4)) )
c = a * b
c ergibt: 
[[ 5  9 15]
 [10 16 20]
 [ 4  7 11]
 [ 7 11 13]]

Matplot

https://matplotlib.org 
sudo apt install python3-matplotlib

import numpy as np
from matplotlib.pyplot import *

zahlen = np.arange(0.0, 2*np.pi, 0.1) # von 0 bis 2*pi in 0.1-Schritten
sinvec = np.sin(zahlen)
plot(zahlen, sinvec)
show()
Mit dem Aufruf von plot wird ein Graph erstellt, aber noch nicht angezeigt. Die Parameter sind das Array für die X-Achse und das Array für die Y-Achse. Beide Arrays müssen die gleiche Länge haben.

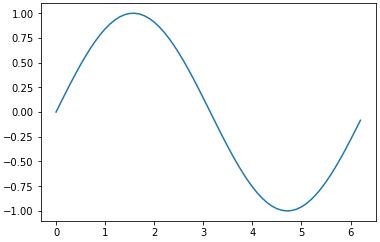
Benamte Parameter:

Weitere Funktionen von pyplot: